הסבר על הפתרון: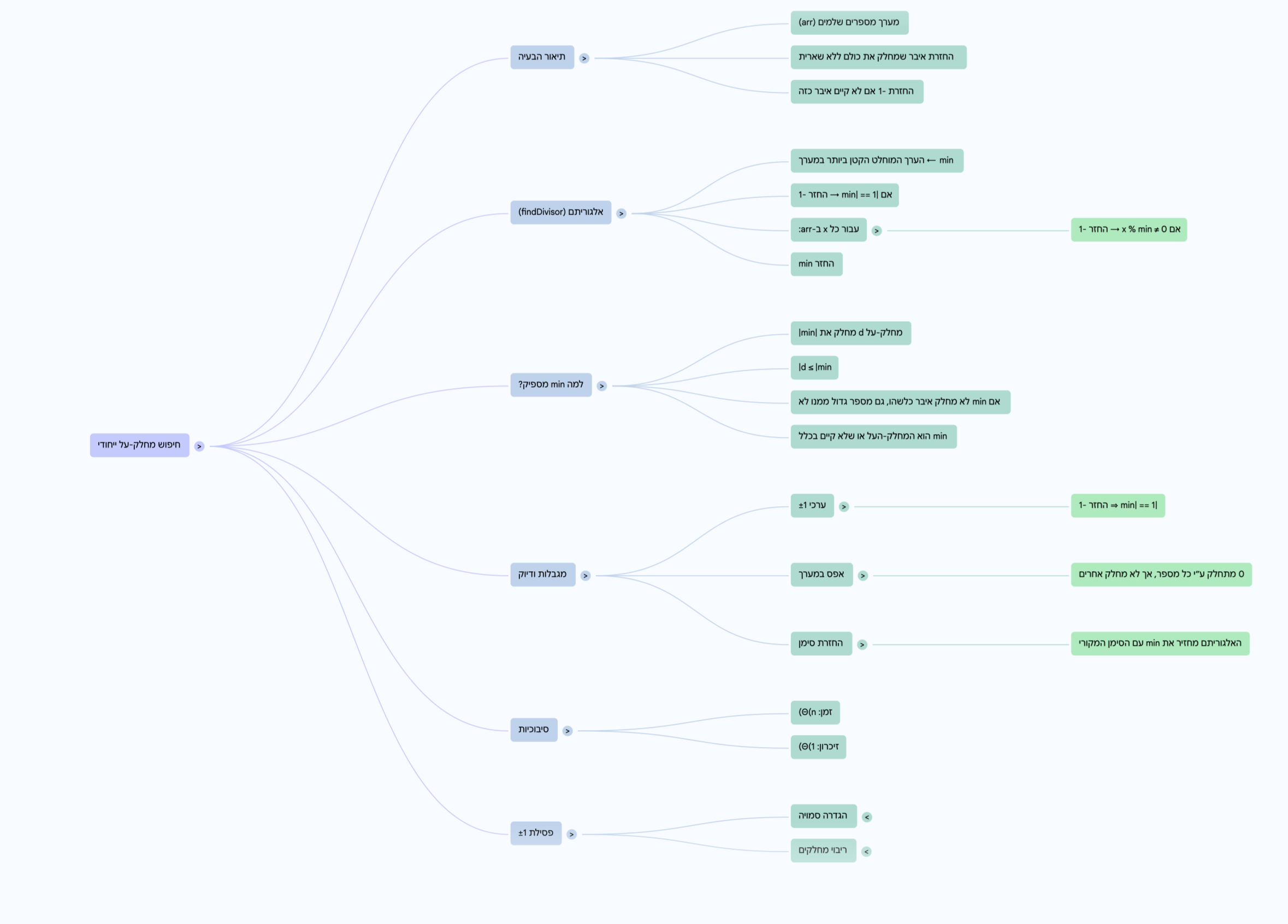

פודקסט הסבר על הפתרון:

מדריך למידה: אלגוריתם למציאת מחלק-על ייחודי במערך

חידון (10 שאלות קצרות)

1. מהי המטרה של האלגוריתם findDivisor?
2. מה האלגוריתם מחזיר אם לא נמצא איבר שמחלק ללא שארית את כל שאר האיברים במערך?
3. איזה ערך במערך נבחר בתור מועמד פוטנציאלי למחלק-על? מדוע?
4. מדוע האלגוריתם בודק את הערך המוחלט של המועמד הפוטנציאלי לפני תחילת הבדיקות?
5. מהי סיבוכיות הזמן של האלגוריתם? מהי סיבוכיות הזיכרון?
6. כיצד האלגוריתם מתמודד עם מצב בו יש אפס במערך? מה קורה ומה מוחזר?
7. מה קורה אם במערך נמצאים גם המספר 1 או ‎-1? מדוע?
8. מהם התנאים לקיום "מחלק על יחיד" במערך?
9. הסבירו בקצרה את הטיעון הלוגי מאחורי העובדה שאפשר להסתפק בבדיקת האיבר בעל הערך המוחלט הקטן ביותר.
10. מה צריך לעשות אם נדרש להחזיר מחלק חיובי בלבד, למרות שהאלגוריתם יכול להחזיר מחלק שלילי?

מפתח תשובות לחידון

1. המטרה של האלגוריתם findDivisor היא למצוא את האיבר היחיד במערך שמחלק ללא שארית את כל האיברים האחרים, כולל את עצמו.
2. אם לא נמצא איבר כזה, האלגוריתם מחזיר ‎-1.
3. האלגוריתם בוחר את האיבר במערך בעל הערך המוחלט הקטן ביותר כמועמד פוטנציאלי למחלק-על, מכיוון שאם קיים מחלק-על, הוא חייב לחלק את האיבר הקטן ביותר בערכו המוחלט.
4. האלגוריתם בודק את הערך המוחלט של המועמד הפוטנציאלי כדי לבדוק אם הוא שווה ל-1. אם כן, הוא מחזיר ‎-1 מכיוון ש-1 או ‎-1 מחלקים כל מספר ואינם מספקים מידע ייחודי על המערך.
5. סיבוכיות הזמן של האלגוריתם היא Θ(n) וסיבוכיות הזיכרון היא Θ(1).
6. אם 0 הוא ה-min, הלולאה תיכשל כיוון שאפס לא יכול לחלק אף מספר אחר מלבד אפס בעצמו. האלגוריתם ימצא איבר ש-x % min != 0 ויחזיר ‎-1.
7. אם במערך נמצאים גם המספרים 1 או ‎-1 והם ה-min, האלגוריתם יחזיר ‎-1. זאת משום שהם מחלקים כל מספר ולכן לא מייצגים מחלק "ייחודי".
8. התנאים לקיום "מחלק על יחיד" במערך הם: קיים איבר (שערכו המוחלט גדול מ-1) שמחלק ללא שארית את כל האיברים האחרים במערך.
9. הטיעון הוא שאם קיים מחלק-על כלשהו, הוא חייב גם לחלק את האיבר בעל הערך המוחלט הקטן ביותר. לכן, אם האיבר בעל הערך המוחלט הקטן ביותר עצמו לא מחלק את כל שאר האיברים, שום מספר אחר לא יוכל להיות מחלק-על.
10. אם נדרש להחזיר מחלק חיובי בלבד, יש לעטוף את החזרת ה-min בפונקציה Math.abs() כדי להבטיח שהתוצאה תהיה תמיד חיובית.

שאלות לחיבור (פורמט חיבור)

1. הסבירו את העקרונות המתמטיים העומדים בבסיס האלגוריתם findDivisor. התמקדו בהסבר מדוע מספיק לבדוק רק את האיבר בעל הערך המוחלט הקטן ביותר.
2. נתחו את סיבוכיות הזמן והזיכרון של האלגוריתם findDivisor. הסבירו מדוע האלגוריתם יעיל מבחינת משאבים.
3. דמיינו שאתם כותבים תיעוד טכני עבור האלגוריתם findDivisor. הסבירו כיצד יש להשתמש באלגוריתם, מהן המגבלות שלו ומתי הוא עלול להחזיר תוצאה שגויה.
4. הציעו דרכים לשיפור האלגוריתם findDivisor, תוך התייחסות למקרים קצה שונים (למשל, מערכים גדולים מאוד, מערכים עם ערכים קיצוניים).
5. השוו את הגישה של האלגוריתם findDivisor לגישות אחרות לפתרון בעיית מציאת מחלקים משותפים. מהם היתרונות והחסרונות של כל גישה?

מילון מונחים

• מחלק-על (Super-divisor): איבר במערך שמחלק ללא שארית את כל האיברים האחרים במערך (כולל את עצמו).
• ערך מוחלט: המרחק של מספר מאפס, ללא תלות בסימן שלו (לדוגמה, הערך המוחלט של ‎-5 הוא 5).
• שארית: הערך שנותר לאחר חילוק שני מספרים שלמים (לדוגמה, השארית של 7 חלקי 3 היא 1).
• סיבוכיות זמן: מדד לכמות הזמן שלוקח לאלגוריתם לרוץ, כפונקציה של גודל הקלט (במקרה זה, גודל המערך).
• סיבוכיות זיכרון: מדד לכמות הזיכרון שאלגוריתם משתמש בה, כפונקציה של גודל הקלט.
• Θ(n): סימון המתאר סיבוכיות ליניארית, כלומר, זמן הריצה גדל באופן ישר לגודל הקלט.
• Θ(1): סימון המתאר סיבוכיות קבועה, כלומר, זמן הריצה אינו תלוי בגודל הקלט.
• מחלק טריוויאלי: מחלק שאינו מספק מידע ייחודי (לדוגמה, 1 ו-‎-1 תמיד מחלקים כל מספר).

הפתרון:

public class Start {
    public static int findDivisor(int[] arr) {
        int min = Integer.MAX_VALUE;
        for (int i = 0; i < arr.length; i++) {
            if (Math.abs(arr[i]) < Math.abs(min))
                min = arr[i];
        }
        for (int i = 0; i < arr.length; i++) {
            if (arr[i] % min != 0 || Math.abs(min) == 1)
                return -1;
        }
        return min;
    }


    public static void main(String[] args) {
        int[][] testCases = {
                {2, 4, 6, 8, 10}, // מחלק משותף מינימלי: 2
                {-3, -6, -9}, // מחלק משותף מינימלי: 3
                {5, 10, 20}, // מחלק משותף מינימלי: 5
                {7, 14, 21, 28}, // מחלק משותף מינימלי: 7
                {1, 2, 3, 4}, // אמור להחזיר -1 כי 1 מחלק הכל
                {3, 7, 11}, // אמור להחזיר -1 כי אין מחלק משותף
                {-2, -4, -6}, // מחלק משותף מינימלי: 2
                {Integer.MAX_VALUE, Integer.MAX_VALUE}, // מחלק משותף: Integer.MAX_VALUE
                {-1, -2, -3} // אמור להחזיר -1
        };

        int[] expectedResults = {2, 3, 5, 7, -1, -1, 2, 0, Integer.MAX_VALUE, -1};

        for (int i = 0; i < testCases.length; i++) {
            int result = findDivisor(testCases[i]);
            System.out.println("Array number: " + (i + 1) + ": " + result);

        }
    }
}